毎度、小2の塾の小難しい問題と格闘している、偏差値40公立高校卒の母です。
今日は、
「これ、こんなに簡単に解けるの?!」
という問題にまた出会った話です。

こういう式を見たことがありませんか?
浜学園の公開学力テストや、馬渕の公開模試でもお目にかかる問題です。
小1で、この短いバージョンも練習したことがあります。
5〇2〇7=10
このような短い問題を馬渕キッズクラブでも練習しました。
短い式ならチャチャッと解けるのですが、
こう長い式になると解くのに時間がかかります。
目からウロコ、簡単な解き方

この写真は、私が未等式を必死で解いたものです。
メッチャ計算しまくっています。
恥ずかしいですがお見せします。
答えにたどり着くまでに10分かかった上に、なんと不正解でした(泣)
でも、これが秒で解けるってご存じでしたか?
ご存じの方は「この人、そんなことも知らなかったのか~」と笑ってください。

この法則を使えば、30秒あれば解けます。
他の式も試してみてください。

小4になると、和差算で線分図を使って解く方法もありますが、
絶対こっちのほうが速くて正確です。
浜学園の説明会で聞いた「いいから、やってみなさい」

ここで息子に質問されたのは、
「20引きたいのに、8+2=10だけ引けばいいってどうして?」
分かるよその質問。母も思いましたもん。
でもね、これってこういう問題と似てるんですよ。
↓
お姉さんが、おはじきを44個持っていて、妹は24個持っています。
二人のおはじきの数を同じにするには、
お姉さんは、妹に何個あげればいいですか?
44-24=20
だから、
妹に10個あげるとちょうど同じになる。
答え 10個
↑ちょいちょい公開模試に出る問題です。
「だから、こんな感じで、20引きたかったら、10になる数字を探して引き算したらいいよ」
と言うと、
息子は「あ~そういうことか」なんて、分かった風にいってます。
ホントに分かってる?? まあいいか、とにかく、
「いいから、やっとけ」
もう、これにつきます。
以前、浜学園の説明会に参加した時に、こんな話を聞きました。
「考え込んでしまう子もいるし、
分からない事は完璧に理解したがる子もいます。
そういう子には、場合によって
『いいから、この方法でやってみて』
と指導することがあります」
浜学園の学園長の橋本憲一先生も、著書でこうおっしゃっていました。
「今、分からなくても、
来年分かるから、あせらなくていい」

浜学園の先生方がおっしゃっているのは、この未等式よりも難問の事だとは思いますが、
まずは我が家にとってはこれが一例になります。
法則を当てはめて答えが出るなら、ひとまずそれでやってみよう!
理由は今わからなくても、その内、納得のいく説明が、自分の中で浮かんでくるから。
知っていれば短時間で解けるテクニック

今回のこの問題の解き方を、
知っていると知らないでは大きく時間が変わりますし、答えも間違いにくいです。
素早く解けて、正解率が高い。
そういうテクニックはきっとたくさんあります。
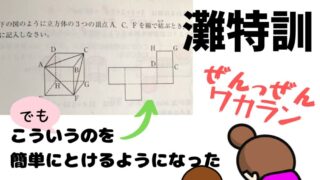
小4の灘特訓で習ったのは、この問題。テクニックを知れば、あっさり解けます。⇓
詳しくはこちらの記事で⇓
例えば、正解だった問題の解説は読まないという方もいるでしょうが、
是非一度、解説には目を通してみてください。
「こんな簡単な解き方あるんだ」
「こっちの方が、分かりやすい」
そんな出会いがあります。
なんだか得した気分になるものです。
そういう意味でも、低学年の内でも、問題集をこなして、いろんな問いを体験するのがいいことだと思うんですよね。
(基礎も大事なのも間違いないですが!)
- 正解でも解説はチェック!良いテクニックに出会えるかも!
- 「いいからやってみて」も大事。
皆さんも、ナイスなテクニックに出会えたらいいですね!
読んで下さってありがとうございました。
ーーーーーーーーーーーーー
【この記事を書いた人】
とろろ
四国の超絶イナカの公立高校卒業。同じ田舎から、
慶応義塾大学に進学したイトコと、その家庭と叔母を隣で見続ける。
高齢出産で産んだ我が子は、どんくさく、運動もダメ。それなら、叔母のように、子どもに学びを身に付けさせようと決意し5年。
中学受験を目指し、塾や家庭学習の事を書いています。
ーーーーーーーーーーーーー